Truth table
A truth table is a mathematical table used in logic — specifically in connection with Boolean algebra, boolean functions, and propositional calculus — to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their logical variables. In particular, truth tables can be used to tell whether a propositional expression is true for all legitimate input values, that is, logically valid.
"The pattern of reasoning that the truth table tabulates was Frege's, Peirce's, and Schröder's by 1880. The tables have been prominent in literature since 1920 (Lukasiewicz, Post, Wittgenstein)" (Quine, 39). Lewis Carroll had formulated truth tables as early as 1894 to solve certain problems, but his manuscripts containing his work on the subject were not discovered until 1977 [1]. Wittgenstein's Tractatus Logico-Philosophicus uses them to place truth functions in a series. The wide influence of this work led to the spread of the use of truth tables.
Truth tables are used to compute the values of propositional expressions in an effective manner that is sometimes referred to as a decision procedure. A propositional expression is either an atomic formula — a propositional constant, propositional variable, or propositional function term (for example, Px or P(x)) — or built up from atomic formulas by means of logical operators, for example, AND ( ), OR (
), OR (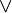 ), NOT (
), NOT ( ). For instance,
). For instance,  is a propositional expression.
is a propositional expression.
The column headings on a truth table show (i) the propositional functions and/or variables, and (ii) the truth-functional expression built up from those propositional functions or variables and operators. The rows show each possible valuation of T or F assignments to (i) and (ii). In other words, each row is a distinct interpretation of (i) and (ii).
Truth tables for classical logic are limited to Boolean logical systems in which only two logical values are possible, false and true, usually written F and T, or sometimes 0 or 1, respectively.
Applications of truth tables in digital electronics
In digital electronics (and computer science, fields of engineering derived from applied logic and math), truth tables can be used to reduce basic boolean operations to simple correlations of inputs to outputs, without the use of logic gates or code. For example, a binary addition can be represented with the truth table:
A B | C R
1 1 | 1 0
1 0 | 0 1
0 1 | 0 1
0 0 | 0 0
where
A = First Operand
B = Second Operand
C = Carry
R = Result
This truth table is read left to right:
- Value pair (A,B) equals value pair (C,R).
- Or for this example, A plus B equal result R, with the Carry C.
Note that this table does not describe the logic operations necessary to implement this operation, rather it simply specifies the function of inputs to output values.
In this case it can only be used for very simple inputs and outputs, such as 1's and 0's, however if the number of types of values one can have on the inputs increases, the size of the truth table will increase.
http://en.wikipedia.org/wiki/Truth_table



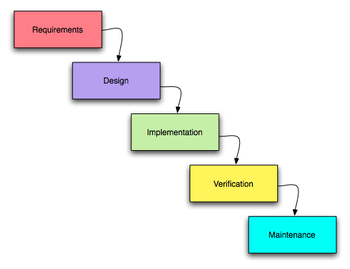


 ),
), 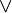 ),
),  ). For instance,
). For instance,  is a propositional expression.
is a propositional expression.